Data Structures You Should Know as a JavaScript Developer
Understanding Data Structures is helpful in all aspects of programming, you don’t need to have a particular use case where you’ll use a…
blog.bitsrc.io
Fernando Doglio, 2020년 7월 27일
데이터 구조를 이해하는 것은 프로그래밍의 모든 측면에서 도움이 된다. 트리나 그래프를 사용할 특별한 경우의 수가 있어서 이것들을 배워볼까 고려할 필요는 없겠지만. 사실 내 개발 인생 15년 동안 적절한 트리 구조를 실행해본적은 한 번도 없는 것 같다. 하지만 이게 어떻게 돌아가는지 이해하는 것은 과거에 여러번 도움이 되었다.
이것들에 대한 지식과 그 구조 및 행동 양식은 우리 분야의 다른 영역에서 추론할 수 있다. 당신한테 그래프가 있다 치고, 이제 하나의 마이크로서비스 기반의 시스템 구성이 어떻게 묘사될 수 있는지 생각해 보라. 이제 다음 그림을 보라:
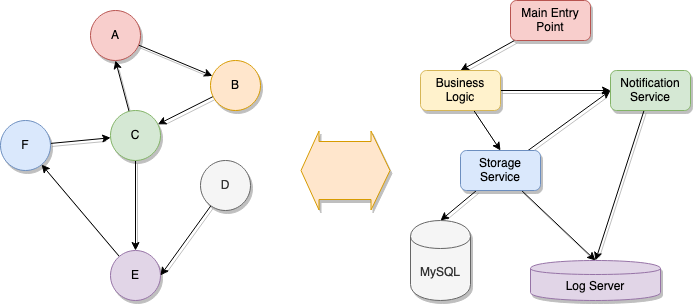
내가 이걸로 뭘 말하려는지 알겠는가? 저 모서리들의 무게가 마치 데이터가 하나의 서비스에서 다른 서비스로 이동하는데 걸리는 시간이라 생각하면, 편중된 그래프라 할지라도 여전히 시스템 구조에 대한 묘사가 될 수 있다.
우리가 여기서 다루려고 하는 다른 구조들에 대해서도 같은 말을 할 수 있다. 그날 그날의 과업에 이것들 중 하나를 실행할 일이 전혀 없을 것 같다 하더라도 이것들을 이해하려고 시간을 할애 해 본다면 그 지식은 미래에 분명 쓸모가 있을 것이다.
그리고 마지막으로 실행에 관한 노트: 이러한 구조들 중 어떤 것들은 가장 기본적인 배열로도 쉽게 표현될 수가 있지만 그 최대 잠재력을 이해하기 위해서는 좀 더 멀리 볼 필요가 있다. 데이터 구조는 데이터를 구성하는 방식만이 아니라 그에 연관된 논리도 가리킨다. 데이터를 삽입하는 방식, 그 안에서는 무슨 일이 벌어지는지, 그 구조에서 데이터를 꺼내는 방법까지도. 그것이 진짜 데이터 구조의 마법과 그 존재의 이유가 있는 곳이다. 그렇지 않으면 우리는 모든 것에 배열을 사용하고 있을 것이다.
. . .
팁: 빗(Bit)(깃헙 - Github)을 사용하여 여러 프로젝트들로부터 재사용 가능한 자바스크립트 컴포넌트들을 공유, 기록, 관리하라. 코드 재사용을 증가시키고, 개발 속도를 높이며 규모 있는 앱들을 만드는 정말 좋은 방법이다.
빗은 노드제이에스, 타입스크립트, 리액트, 뷰, 앵귤러, 그리고 다른 많은 것들도 지원한다.
. . .
행렬
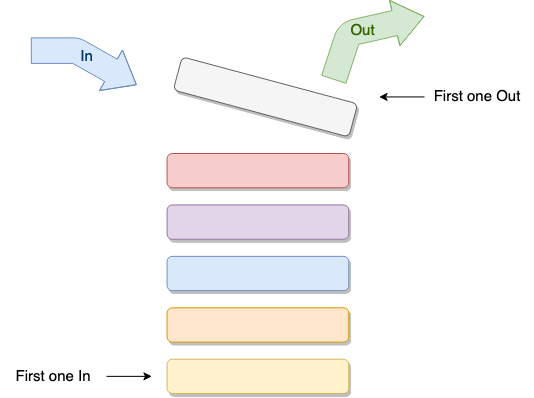
만들어진 순서대로 실행되어야 하는 과업들의 목록을 다룰 필요가 있다면 행렬의 내부 작동을 이용할 수 있다. 이것들은 요소들을 삽입하고 FIFO 접근법: 선입선출에 따라 꺼낼 수 있는 아주 기초적인 구조들이다.
다시 말해, 수퍼마켓에 늘어서 있는 일반적인 행렬을 다루듯이, 행렬에 먼저 들어간 사람이 먼저 서비스 받게 된다.

위의 그림에서 볼 수 있듯이 구조 자체는 매우 단순하고 실행 자체도 꽤나 간단하다. 특히 만약 배열을 기본 데이터 구조로 할 것이라면.
class Queue {
data = []
maxSize
constructor(initialData, maxSize = -1) {
this.data = Array.isArray(initialData) ? initialData : (typeof initialData == "undefined" ? [] : [initialData])
this.maxSize = maxSize
}
isFull() {
return this.maxSize != -1 ? (this.data.length == this.maxSize) : false
}
isEmpty() {
return this.data.length == 0
}
enqueue(item) {
if(this.isFull()) {
return false
}
this.data.push(item)
}
*generator() {
while(!this.isEmpty()) {
yield this.data.shift()
}
}
dequeue() {
const { value, done } = this.generator().next()
if(done) return false
return value
}
}이 실행에서 두 개의 주요한 메소드들은 enqueue 와 dequeue 메소드들이다. 첫번째 것으로 요소들을 행렬에 더할 수 있고 후자에서는 제거할 수 있다.
보시다시피 나는 기본적인 데이터 구조를 위해 배열로 했다. 왜냐면 이것이 두 메소드들을 매우 크게 단순화하기 때문이다. Enqueue 하는 것은 그냥 요소를 배열에 밀어넣는 것과 같고 dequeue는 첫번째 요소를 제거하여 반환하기까지 하는 shift 라는 간단한 불러오기로 해결될 수 있다.
금상첨화로, 아래에 보이는 것과 같은 업무들을 위해 생성 함수가 추가되었다.
const Queue = require('./queues')
let q = new Queue(3, 2)
q.enqueue(1)
q.enqueue(2) //ignored...
let x = 0
while(x = q.dequeue()) {
console.log(x)
}
/*
Prints:
3
1
*/여기서 보여주는 간단한 행렬 외에도 이런 것들을 찾을 수 있다:
- 우선순위 행렬. 우선 값으로 내부 정렬된 요소들을 가지고 있다.
- 순환 행렬. 첫번째 요소를 가리키는 마지막 요소를 가지고 있다.
- 양가 행렬. 요소들을 앞과 뒤 둘 다에서 더하거나 제거할 수 있게 한다. (내게 물어 본다면, 부정행위 같은 것이다!)
스택
스택을 목록에서 두 번째로 넣는 이유는 솔직히 이것이 행렬과 매우 흡사해서 때로는 서로 헷갈리게 하기 때문이다.
하나를 다른 것 위에 놓기 시작하면 이 데이터 구조가 책 무더기 같다 생각할 수 있다. 하나를 원하면 그 위에 놓인 모든 책들을 제거해야 할 것이다. 이런 식으로 데이터를 다루는 것은 FILO, 선입후출로 알려져 있다.
다시 말해 당신이 탁자에 놓는 첫번째 책이, 꺼내게 되는 마지막 것이 될 것이다. 그 위에 놓은 다른 모든 것들을 먼저 치워야 한다는 것을 감안하면.
목록의 첫번째부터 마지막까지 훑으면서 각 요소를 스택에 저장할 수 있기 때문에 스택은 목록의 순서 뒤바꾸기와 같은 것에 유용하다. 그리고 나서 그것들을 꺼낼 수 있고 (선입후출 양식을 따라서) 마지막은 원래 목록의 첫번째 요소가 될 것이다.
또 한가지 흥미로운 사례는 우리가 인지하지 못하면서 무수히 보았던 되돌리기다. 만약 어떤 것을 되돌리고 싶다면 당신은 당신의 마지막 동작을 되돌리려 하거나 혹은 한참 전에 일어났던 것을 되돌리기 위해 몇 가지 동작들도 되돌리려 할 것이다. 어느 경우든지, 말 그대로 당신은 하나의 동작 스택에서 그 요소들을 죽이고 있는 것이다.
먼저 되돌리기 스택 예시를 보자:
const Stack = require("./stack.js")
class Operation {
constructor(val) {
this.value = val
}
}
class Add extends Operation {
apply(value) {
return value + this.value
}
undo(value) {
return value - this.value
}
}
class Times extends Operation {
apply(value) {
return value * this.value
}
undo(value) {
return value / this.value
}
}
/** Operations Stack **/
class OpsStack {
constructor() {
this.value = 0
this.operations = new Stack()
}
add(op) {
this.value = op.apply(this.value)
this.operations.add(op)
}
undo() {
if(this.operations.isEmpty()) {
return false
}
this.value = (this.operations.pop()).undo(this.value)
}
}
let s = new OpsStack()
s.add(new Add(1))
s.add(new Add(1))
s.add(new Times(2))
console.log("Current value: ", s.value)
s.undo()
s.undo()
console.log("Final value: ", s.value)
우리가 어떻게 맞춤 스택을 사용하고 있는지 볼 수 있다. 하나는 전통적인 것을 활용하지만 또한 평행 값의 뒤도 밟고 있다. 작동은 모두 두 가지 메소드를 가진 클래스로 표현되었는데, 작동을 효율적으로 하게 하는 apply와 그 반대 동작을 구현하는 undo다. 우리의 맞춤 스택도 undo 메소드를 가지고 있는데 모든 작동들이 저장되어 있고 그 효과들을 하나씩 되돌릴 수 있는 스택 구조를 이용하고 있다. 위의 코드 실행 결과는:
Current value: 4
Final value: 1
그리고 아마 예상했겠지만 스택의 실행은 이전의 행렬 클래스와 거의 동일하다.
module.exports = class Stack {
data = []
maxSize
constructor(initialData, maxSize = -1) {
this.data = Array.isArray(initialData) ? initialData : (typeof initialData == "undefined" ? [] : [initialData])
this.maxSize = maxSize
}
isFull() {
return this.maxSize != -1 ? (this.data.length == this.maxSize) : false
}
isEmpty() {
return this.data.length == 0
}
add(item) {
if(this.isFull()) {
return false
}
this.data.push(item)
}
*generator() {
while(!this.isEmpty()) {
yield this.data.pop()
}
}
pop() {
const { value, done } = this.generator().next()
if(done) return false
return value
}
}유일한 차이를 발견할 수 있는가? 27번줄을 확인해보라. 다행스럽게 자바스크립트의 배열 클래스는 pop 메소드만 제공해주기 때문에 우리가 기대하는 것을 한다: 배열에서 마지막으로 더해진 것을 제거하여 반환함.
스택과 행렬은 멋지지만 좀 더 복잡하지만 훨씬 더 강력하고 다재다능한 것을 살펴보는 게 어떨까?
트리
트리가 무엇인지, 어떻게 형성되는지 무엇을 위해 사용될 수 있는지를 정의하기 위한 이론은 매우 많다. 거기로는 들어가지 않을 것인데 왜냐하면 솔직히 말해서 이론을 원한다면 그냥 위키피디아나 그것에 대해 자세히 다룬 많은 책들 중 하나를 치면 된다.
그 대신 나는 축약된 버전을 주어 얘네들이 뭘 할 수 있는지 맛을 볼 수 있게 할 것이고, 만약 당신이 이것들을 좋아하게 된다면 원하는 만큼 더 깊게 파면 된다.
트리는 기본적으로 부모 노드 및 한 부모와 연결된 여러 자식 노드들에 의해 형성된 재귀적으로 정의된 구조다. 내가 말했던 것처럼, 이 자식 노드는 각각 다른 자식의 부모 노드가 될 수 있다는 점에서 재귀적인 정의이다.
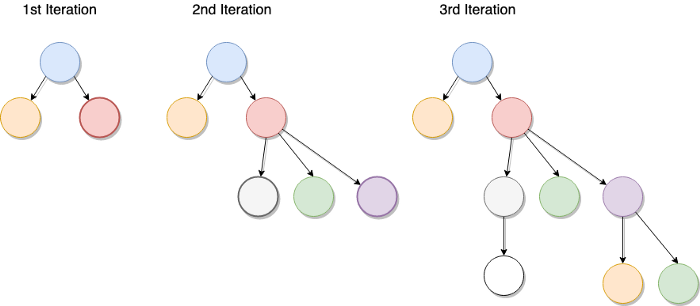
트리가 어떻게 자라는지 보여주는 위의 그림을 보면 메모할만한 몇 가지 흥미로운 점들이 있다:
- 형제 노드들(즉 같은 부모를 가진 노드들)은 서로 연결되어 있지 않다.
- 트리는 일반적으로 아래로 자라면서 구현된다.(보통 트리는 위로 자란다는 것과는 반대로)
- 노드들은 자기 자신에 연결될 수 없다.(이상하게 들린다는 건 알지만 그래프 얘기할 때까지 기다리길)
미래의 명명법을 명확히 하기 위해서 트리의 다른 섹션들은 다음과 같이 알려져 있다:
- 뿌리 노드 / 부모 노드: 자식을 아래에 두고 있는 노드
- 나뭇잎 노드: 연관된 자식 노드가 없는 노드
- 모서리: 두 노드의 연결
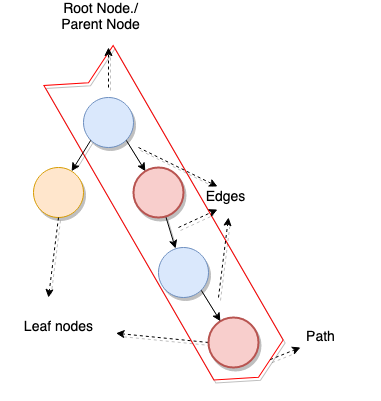
아래의 그림으로부터 우리는 몇 가지를 더 정의할 수 있다:
- 경로(Path): 뿌리 노드에서 목적지 노드로 가기 위해 필요한 노드의 목록
- 나무의 높이: 뿌리 노드와 가장 멀리 있는 나뭇잎 노드 사이의 가장 긴 경로를 형성하는 노드들의 양
그 말을 했으니 말인데, 구조로부터 데이터 삽입과 추출과 연관된 논리에 의존하는 트리들의 종류는 여러 가지가 있다.
- 2진법 트리: 부모 노드가 최대 두 개까지의 자식만을 가질 수 있는 트리다(그래서 2진법임). 이런 트리 종류를 위한 잠재적인 사용 예시는 압축 알고리즘이다. 이것들은 또한 2진법 검색 트리를 생성하는 데에도 쓰인다.
- 2진법 검색 트리: 2진법 트리의 한 특별한 종류로, 요소를 트리에 삽입할 때 논리가 그것을 뿌리 노드의 값과 비교하여 그것보다 작으면 왼쪽 자식을 확인하고 그렇지 않으면 오른쪽 자식을 확인한다. 이 논리는 당신이 나뭇잎 노드를 찾아서 그 자식으로 그 값을 연결하거나 한 부모의 자식이 될 수 있는 자리를 찾을 때까지 반복된다. 이것의 전형적인 사례는 매우 적은 노력으로 정렬된 구조를 유지하길 원할 때이다.
- 깊이 우선 검색(DFS - Depth First Search): 이것은 무엇인가를 찾기 위해 트리를 훑어 나가는 방식이다. 먼저 왼쪽 전체를 가로지르고, 그 후 마지막으로 방문했던 부모를 거슬러 올라가 오른쪽 하위 트리로 넘어간다.
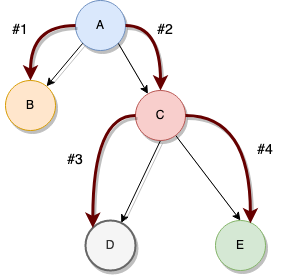
위의 그림을 보면 만약 당신이 각 노드의 값을 출력하려고 거기에 가면 A->B->C->D->E의 순서로 얻을 것이다. 노드의 순서는 DFS 메소드에 의해 정해진다:
1. Print A
2. Go to the left child
3. Print B
4. No more children, so backtrack to A
5. Go to the right child
6. Print C
7. Go left
8. Print D
9. No children, so back to C
10. Go right
11. Print E
12. End
반대 순서로 훑을 수도 있다. 오른쪽 먼저 그리고 왼쪽으로. 이 알고리듬은 미로와 같은 위상 구현(다른 사례들 중에서)을 탐색하려 하거나 뿌리노드 (입구) 및 출구를 표현하는 노드 사이의 경로를 찾으려 할 때, 트리와 그래프 둘 다와 함께 사용될 수 있다.
되게 뭔가 많은 거 같이 들리지만, 내가 2진법 검색 트리(트리 종류들 중 내가 제일 좋아하는 것 중 하나)를 어떻게 실행할지 예시를 보여주어 그것이 그다지 복잡하지 않고 실제로 매우 유용함을 알수 있게 해주겠다.
하지만 먼저, 우리의 나무 구조를 어떻게 사용할지 보여주어 우리가 무엇을 실행시키는지 좀 더 이해할 수 있도록 하겠다.
const Tree = require("./bst")
const t = new Tree()
t.add(10)
t.add(8)
t.add(11)
t.add(23)
t.add(1)
t.add(9)
t.print()
/*
Prints:
1
8
9
10
11
23
*/이것이 삽입 구조에서 정렬의 장점이다. 숫자를 더하면서 정렬하므로, 출력을 원하면 그냥 그 구조를 훑기만 하면 되는 문제다. 실행을 보자:
class BinaryTreeNode {
constructor(value) {
this.value = value
this.left_child = null
this.right_child = null
}
compare(v) {
if(this.value > v) return -1
if(this.value == v) return 0
if(this.value < v) return 1
}
}
module.exports = class BST {
constructor() {
this.root_node = null
}
/**
If root node is empty (tree is empty), elem becomes root node
If elem is lower than root node, switch to the left sub-node and check if it's empty
If it's empty, elem becomes left sub node
If not, keep traversing this way
If elem is higher or equal to root node, switch to right sub-node and check if it's empty
if it's empty, elem becomes the right sub-node
If not, keep traversing this way
*/
add(elem) {
if(!this.root_node) {
this.root_node = new BinaryTreeNode(elem)
return
}
let inserted = false
let currentNode = this.root_node
do {
let comp = currentNode.compare(elem)
if(comp == -1) {
if(!currentNode.left_child) {
currentNode.left_child = new BinaryTreeNode(elem)
inserted = true
} else {
currentNode = currentNode.left_child
}
}
if(comp != -1) {
if(!currentNode.right_child) {
currentNode.right_child = new BinaryTreeNode(elem)
inserted = true
} else {
currentNode = currentNode.right_child
}
}
} while (!inserted)
}
inorder(parent) {
if(parent) {
this.inorder(parent.left_child)
console.log(parent.value)
this.inorder(parent.right_child)
}
}
print() {
this.inorder(this.root_node)
}
}코드가 길지만 여기서 가장 길고 복잡한 메소드는 add 메소드다. 이것은 주로 do...while 루프로 이루어져 트리를 훑으며 새 값을 놓을 빈 공간을 찾는다. find나 remove 메소드 같은 것을 실행하고 싶을 다른 동작들도 있다.
inorder 메소드는 그냥 훑는 순서(왼쪽, 가운데, 그리고 오른쪽)를 빠르게 재귀 실행한 것이다. 왼쪽과 오른쪽의 자식들을 맞바꿈으로써 아마도 이것을 반대 순서(또는 후위운행법)로 가로지를 수도 있다.
이제 트리의 형: 그래프에게로 넘어가자.
그래프
그래프는 부모 자식이 없고 아무 노드나 다른 아무 노드에게로(본인 포함하여!) 연결될 수 있다는 점에서 제한이 적은 트리다.
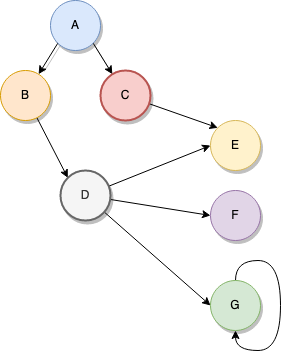
그래프는 주체들이 서로 연결될 수 있는 거의 모든 시나리오들을 구현하는데 사용될수 있기 때문에 매우 다재다능하다. 그리고 나는 네트워크 레이아웃에서부터 마이크로서비스 기반 시스템 구조, 실생활의 지도들, 당신이 정말 상상할 수 있는 모든 것에 해당하는 범위의 사례들을 말하고 있는 것이다.
이것은 너무나 많아서, 그래프 개념에 근거한 전체 데이터베이스 엔진들이 있다. (예를 들어 Neo4J는 매우 인기 있는 것이다) 모서리, 노드, 경로 등과 같은 트리로부터의 모든 개념들은 여기에도 여전히 유효하다.
여기 깊이 우선 검색 훑기(이것이 무엇인지 이해하기 위해 트리 섹션을 확인하라)를 실행하는 방법을 보여주는 메소드를 포함, 그래프를 자바스크립트로 빠르고 지저분하게 실행한 것이 있다.
class Node {
constructor(value) {
this.value = value
this.links = []
}
linkTo(node, weight) {
this.links.push(new Link(this, weight, node))
}
}
class Link {
constructor(a, weight, b) {
this.left = a;
this.weight = weight
this.right = b
}
}
class Graph {
constructor(root_node) {
this.root_node = root_node
this.dfs_visited = new Set();
}
dfs(starting_node) {
if(!starting_node) starting_node = this.root_node
let node = starting_node
console.log(node.value);
this.dfs_visited.add(node);
node.links.forEach( neighbour => {
if (!this.dfs_visited.has(neighbour.right)) {
this.dfs(neighbour.right);
}
})
}
}필수적으로, 각 노드는 두 노드들 사이의 관계를 나타내는 "링크들"의 목록을 가지고 있다. 그리고 사실 추가 보너스로 이것들은 편중된 링크들인데, 그 말은 당신이 원하는 것은 무엇이든 구현하는 값을 그 관계에 추가할 수 있다는 뜻이다. (예를 들어, 네트워크 연결의 ns 지연, 두 위치 사이의 트래픽의 양, 또는 말 그대로 무엇이든 당신이 원하는 것)
dfs 메소드는 우리의 그래프를 훑는 것을 담당하여 우리가 각 노드를 확실히 한 번만 방문하게 할 것이다. 여기 이것을 어떻게 사용하는지 예시가 있다.
//Define the nodes
let A = new Node("A")
let B = new Node("B")
let C = new Node("C")
let D = new Node("D")
let E = new Node("E")
let F = new Node("F")
let G = new Node("G")
//Define how each node is related to others
A.linkTo(B, 1)
A.linkTo(C, 2)
B.linkTo(D, 1)
C.linkTo(E, 10)
D.linkTo(E, 10)
D.linkTo(F, 1)
D.linkTo(G, 1)
G.linkTo(G, 1)
let g = new Graph(A)
//Traverse the graph
g.dfs()위의 예시는 이 섹션 시작에서 보여주었던 그래프를 나타낸다. G의 본인과의 관례를 포함해서! 그 출력은 이런 식일 것이다.
A
B
D
E
F
G
C
다시 말해, 모든 노드는 오직 한 번만 방문한다. 그래프로 더 흥미로운 것들, 다익스트라의 알고리듬을 실행해서 두 노드들 사이의 가장 짧은 경로를 찾아내거나 AI 루트로 가서 신경망을 실행하는 것과 같은 것들을 할 수 있다. 그래프들로 상상하는 것 모두를 할 수 있으니, 아직 바로 그렇게 물리지 말고 그것들에게 기회를 주어라.
해시맵
이 글에서 내가 다룰 마지막 데이터 구조는 해시맵이다. 필수적으로 이것은 키-값 쌍을 저장하고 빠르게 꺼낼 수 있게 해준다.(어떤 사람은 이것이 복잡성 단계에서 0(1)인 최고의 시나리오를 가지고 있다고 하니 정말 놀랍다)
이것을 고려해 봐라: 메모리에 저장해야 하는 키-값 쌍이 300개가 있다. 쉽게 배열에 의지할 수 있다. 문제는? 만약 어떤 특정 값을 빼내고자 한다면 그 것을 찾아 전체 배열을 훑어야 한다. (이것은 당신이 찾은 것이 마지막에 있다고 가정했을 때의 최악의 시나리오이다) 물론 300개의 요소들은 큰 일은 아니지만 1,000,000 요소들의 목록 안에서 하나의 요소를 찾아야 되는 이론적인 경우의 수를 고려해 보자. 시간이 꽤나 걸릴 것이고 기초 숫자가 계속 증가한다면 배열은 이 경우에 점점 더 효용성이 적어진다.
해시 맵은 반면에 키를 활용하여 정해진 시간 안에 값에 빠르게 접근할 수 있게 하는 구조를 생성하게 해준다. 자바스크립트에서 무작위 속성들(즉 우리의 키들)을 추가하는 데 사용할 수 있는 객체 직역이 있다는 것을 고려하면 해시맵의 실행은 상당히 쉽다. 숫자 키들이 사용되게 해주는 해시맵의 빠른 실행이 여기 있다.
class HashMap {
constructor() {
this.map = {}
}
hash(k) {
return k % 10
}
add(key, value) {
let k = this.hash(key)
if(!this.map[k]) {
this.map[k] = []
}
this.map[k].push(value)
}
get(key) {
let k = this.hash(key)
return this.map[k]
}
}
let h = new HashMap()
h.add(10, "hello")
h.add(100001, "world")
h.add(1, "this is a string")위 스크립트로부터의 출력은:
HashMap {
map: { '0': [ 'hello' ], '1': [ 'world', 'this is a string' ] }
}
"world"와 "this is a string"둘이 어떻게 동일한 키와 연관되었는지를 보라. 이것이 해시 충돌로 알려진 그것이다. 나의 hash 메소드는 원래 키가 무엇인지에 상관 없이 어떠한 주어진 시간에도 최대 10개의 키만 보유하는 것을 확실히 하도록 단순히 mod 10을 하고 있다. 이것은 메모리의 양이 제한적일 때나 어떠한 이유로 키들에 대한 엄격한 제어를 유지해야 할 필요가 있을 때 도움이 된다. 해싱 메소드를 실행하는 방식이 해시 맵이 결국 얼마나 효율적인 것으로 남을지를 결정하게 될것이다.
잘 실행되면, 이 구조는 아주 효율적이어서 데이터베이스 인덱싱(일반적으로 빠른 검색 작업을 하고 싶을 때 필드들을 인덱스로 설정한다) 그리고 심지어 캐시 실행, 허용, 다시, 캐시된 내용을 꺼내기 위한 빠른 검색 작업과 같은 시나리오들에 널리 사용된다. 예상 했겠지만 빠르고 반복되는 검색을 찾고 있다면 이것은 위대한 구조다.
결론
데이터 구조들을 일일 과업에 사용하든지 아니든지 이것들을 이해하는 것은 비록 자신이 모르고 있다 하더라도 이미 당신이 가지고 작업하고 있는 패턴들에 눈이 트이게 하기 때문에 매우 중요하다.
위의 실행들을 가지고 놀면서 재미를 찾고 당신의 것을 만들어라. 아마 그 과정에서 당신이 가지고 있지만 어떻게 풀어야 할지 모르겠는 문제들에 대한 해결책이 나올 수도 있다!
어느 것이 당신이 가장 좋아하는 데이터 구조인가? 아래에 댓글을 남겨 모두와 공유해주길 바란다.
그때까지, 다음에 봅시다!
'웹개발' 카테고리의 다른 글
| 2020년에 웹 개발자가 되는 방법 - 완성 가이드 (0) | 2020.08.01 |
|---|---|
| 리액트를 사용하여 마이크로프론트엔드 개발하는 방법: 단계적인 가이드 (0) | 2020.07.29 |
| 자바스크립트로 더 깔끔한 코드를 쓰는 방법 (0) | 2020.07.27 |
| 리액트에서 스타일드-컴포넌츠를 사용하는 방법 (0) | 2020.07.24 |
| 디자인 와이어프레임을 접근성 있는 HTML/CSS로 옮기기 (0) | 2020.07.23 |